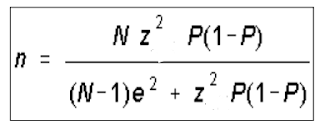TEMA 8: TEORÍA DE MUESTRAS: tipos de muestreo. Teoría de la estimación. Tamaño de la muestra.

ESTIMACIÓN E INFERENCIA ESTADÍSTICA. TÉCNICA DE MUESTREO.

 El proceso de inferencia consiste  en medir un parámetro realizando una selección preferiblemente aleatoria, una muestra mediante muestreo y una vez que calculo el estimador de ese parámetro hago la inferencia, es decir, puedo aproximarme al conocimiento de ese parámetro. Las técnicas de muestreo es un método tal que al escoger un grupo pequeño de una población podamos tener un grado de probabilidad de que ese pequeño grupo posea las características de la población que estamos estudiando. Además de la técnica debemos de tener en cuenta el tamaño de la muestra para estimar de una población. Esta va a depender  de la varianza y del tamaño de la población, del error aleatorio y de la mínima diferencia entre los grupos de comparación que se considera importante  en los valores de la variable a estudiar. Su fórmula es:

n = z² x S² / e²

• Z es el valor que depende del nivel de confianza 1-α con que se quiere dar a los intervalos calculados a partir de estimadores de esa muestra.
• S² es la varianza poblacional
• e es el error máximo aceptado
• Si tras esta operación se  cumple el resultado N> n (n-1) el cálculo del tamño termina pero si no se cumple, obtendremos el tamaño de la muestra con esta fórmula n'= n/1 + (n/N)

Para calcular el tamaño de una muestra cuando queremos estimar una proporción:

• p es la proporción de una categoría de la variable
• 1-p es la proporción de la otra categoría
• z es el valor que depende del nivel de confianza 1-a
• N es el tamaño de la población
• e es el error máximo aceptado por los investigadores en las diferencias entre los grupos de comparación de la variable a estudiar.

TIPOS DE MUESTREO

No probabilístico: No utilizan el azar por lo que la muestra no es representativa de una población y hay sesgo de selección. El investigador selecciona la muestra siguiendo algunos criterios identificados para los fines del estudio que realiza. Encontramos:

1. Por conveniencia o internacional: en el que el investigador decide, según sus objetivos, los elementos que integrarán la muestra, considerando las unidades “típicas” de la población que desea conocer.
2. Por Cuotas: En el que el investigador selecciona la muestra considerando algunos fenómenos o variables a estudiar, como: Sexo, raza, religión, etc.
3. Accidental: Consiste en utilizar para el estudio las personas disponibles en un momento dado, según lo que interesa estudiar. De las tres es la más deficiente. 

Probabilístico: Introducen el azar por lo que todos y cada uno de los elementos tienen una probabilidad calculable y, por lo tanto, conocida, de ser elegidos para la muestra. Consiste en extraer una parte (o muestra) de una población o universo, de tal forma que todas las muestras posibles de tamaño fijo, tengan la misma posibilidad de ser seleccionadas.

1. Estratificado: Se caracteriza por la subdivisión de la población en subgrupos o estratos, debido a que las variables principales que deben someterse a estudio presentan cierta variabilidad o distribución conocida que puede afectar a los resultados.
2. Por conglomerados: Se usa cuando no se dispone de una lista detallada y enumerada de cada una de las unidades que conforman el universo y resulta muy complejo elaborarla. En la selección de la muestra en lugar de escogerse cada unidad se toman los subgrupos o conjuntos de unidades “conglomerados”. En este tipo de muestreo el investigador no conoce la distribución de la variable. Las inferencias que se hacen en una muestra conglomerada no son tan confiables como las que se obtienen en un estudio hecho por muestreo aleatorio.
3. Sistémico: Similar al aleatorio simple, en donde cada unidad del universo tiene la misma probabilidad de ser seleccionada. Ejemplo: 

          N= 500          N/n =5 será el intervalo para  la selección de cada unidad muestral

          n=100           

     4. Aleatorio simple: Se caracteriza porque cada unidad tiene la probabilidad equitativa de ser                incluida en la muestra: 

      De sorteo o rifa: Desventaja de este método          es que no puede usarse cuando el universo es        grande.        

     Tabla de números aleatorios: más económico        y requiere menor tiempo.

PROBLEMAS PRÁCTICOS

• Predetermina el tamaño de una muestra necesaria para estudiar la meda del nivel de glucosa plasmática de una población. Aceptamos un riesgo de erros del 1% y pretendemos una precisión de 5mg/ dl. En un estudio anterior la desviación típica resultó ser de 15mg. Calcula el tamaño de la muestra. 

e = 5mg/dl                                         

S= 15 mg/dl                                     

riesgo de error 1%  →99% de cconfianza deseada → z= 2`58.                              

n = z² x S² / e²

n = 2’58²  x 15² / 5² = 59`9   ⤑  n= 60 (el tamaño mínimo muestral para garantizar esprexiones de confianza, siempre redondeamos para arriba)

• Predetermina el tamaño de prevalencia de hipertensión en 5000 habitantes. Un estudio piloto mostró prevalencia del 15%, el nivel de confianza es del 95% y la precisión ±5 %. ¿Cuál es el tamaño de la muestra?

N= 5000 (habitantes)

95% → z= 1'96

e= 0'05 (error máx aceptado)

p= 0,15 

1-p= 0'85  

Utilizamos la fórmula cuando queremos estimar el tamaño en una población:

Los sujetos quedeberían meter en la muestra son 189.

Esto ha sido todo por hoy, espero que se haya entendido. 

Hasta la próxima!!

Almu❤

TEMA 7: TEORÍA DE LA PROBABILIDAD: Conceptos básicos. Distribución y reglas básicas de la probabilidad. Teorema de Bayés. Distribución de probabilidad discreta: binomial y de Poisson. Distribución de probabilidad continua: normal o campana de Gauss.

Hoy explicaremos el tema 7 que se centra en la Probabilidad. Espero que os sirva de ayuda este resumen del temario y que lo pongáis en práctica mediante ejercicios. 

Para comunicarnos y entendernos utilizamos el término "Probabilidad" que se expresa mediante un número del 0 al 1 siendo el 1 lo más probable (o también en porcentajes).  Si en nuestros ejemplos no existe la certeza de que ocurra los hechos, existe una esperanza dimensionada y razonable, de que el hecho confirmado se vea anunciado por lo  que nos ayuda a tomar decisiones. Aunque el concepto es simple, ya que se usa de manera intuitiva, su definición es complicada y tiene tres vertientes:

1) PROBABILIDAD SUBJETIVA O PERSONALÍSTICA

La probabilidad mide la confianza que el individuo tiene sobre la certeza de una proposición determinada, este concepto de las probabilidades ha dado lugar al enfoque de análisis de datos estadísticos llamado “estadística bayesiana”

2) PROBABILIDAD OBJETIVA

Probabilidad clásica o “a priori”. Fue desarrollada para resolver juegos de azar por lo que las probabilidades se calculan con un razonamiento abstracto. Por ejemplo, la pobabilidad a “priori” de que salga un As en una baraja de póker (52 cartas) será: P(As)= 4/52= 0’0769= 7’7%.  Inicialmente esa probabilidad real puede no cumplirse pero si repetimos muchas veces el experimento, la frecuencia relativa de un suceso A, cualquiera, tiende a estabilizarse al torno al valor “ a priori”.  Probabilidad de A= Nº de resultados favorables a A ➗ Nº total de resultados posibles

Probabilidad relativa o "a posteriori".  Si el número de determinaciones (repeticiones de un experimento aleatorio) es grande, podemos esperar que la probabilidad observada se acerque a la probabilidad teórica.

La Probabilidad frecuencial = Nº de veces que se obtiene el resultado que se estudia➗ Nº de repeticiones de experimento.

3) EVENTOS O SUCESOS

El conjunto de todos los resultados posibles se llama espacio muestral (S). Se llama suceso o evento a un subconjunto de dichos resultados. Se llama evento complementario de un suceso A, formado por los elementos que no están en A y se denota Ac. Se llama evento unión de A y B, AuB, al formado por los resultados experimentales que están en A o en B (incluyendo todos los que están en ambos). Se llama evento intersección de A y B, A∩B al formado por los elementos que están en A y B. 

También encontramos el TEOREMA DE BAYES que vincula la probabilidad de A dado B con la probabilidad de B dado A.

Distribución de probabilidad en variables discretas:

Binomial

 Es un  modelo matemático de distribución teórica de (la normal es con variables continuas) variables discretas cuando se producen situaciones en las que sólo existen dos posibilidades (cara/cruz; sano/enfermo…). El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente. La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad de A' es 1- p y la representamos por q . 

El experimento consta de un número n de pruebas.

Distribución de Poisson

Se utiliza en situaciones donde los sucesos son impredecibles o de ocurrencia aleatoria. No se sabe el total de posibles resultados. Permite determinar la probabilidad de ocurrencia de un  suceso con resultado discreto.  Es muy útil cuando la muestra o segmento n es grande y la probabilidad de éxitos p es pequeña. Se utiliza cuando la probabilidad del evento que nos interesa se distribuye dentro de un segmento n dado como por ejemplo, distancia, área o volumen o tiempo definido. 

Distribuciones normales

Tipificación de valores en una normal:  

Extrapolando aparecen los principios básicos de las distribuciones normales y podemos tipificar valores de una normal     

 – ± 1S 68,26% de las observaciones

 – ± 2S 95,45% de las observaciones 

 – ± 1,95S 95% de las observaciones   

 – ± 3S 99,73% de las observaciones 

 – ± 2,58S 99% de las observaciones 

La tipificación de la valores se puede realizar sí …  Trabajamos con una variables continuas que

sigue una distribución normal (TLC)  y  tiene más de 100 unidades (LGN).  La tipificación nos permite conocer si otro valor corresponde o no a esa distribución de frecuencia

La tipificación se lleva a cabo mediante esta fórmula:

(Valor determinado - valor de la media del conjunto) / desviación típica.

Hasta la próxima!!

"Todos los triunfos nacen cuando nos atrevemos a comenzar"  

Engene Ware

Almu❤

TEMA 6: REPRESENTACIÓN GRÁFICA DE LA INFORMACIÓN: Representación variables cualitativas y cuantitativas discretas. representación de variables cuantitativas continuas. errores en las representaciones

Las REPRESENTACIONES GRÁFICAS: son una forma rápida de comunicar información numérica (frecuencias), son la imagen de las ideas (barras, histogramas, sectores...), complementan el análisis estadístico, aumentando la información y ofreciendo orientación visual y no reemplaza a las medidas estadísticas que deben ser calculadas

 Normas básicas:  Visualmente claros. Claramente descritos en pie de figura y en texto. Representan gráficamente las conclusiones del estudio. Evitar gráficos confusos, no sobrecargarlos. Representaciones gráficas más empleadas:

Variables cualitativas (dicotómicas o de pocas categorías)

Gráfico de sectores (dicotómicas con pocas categorías): el área de cada sector circular es proporcional a la frecuencia de las categorías de la variable. Solo muestra una variable a la vez. No cometer estos errores: Usar demasiadas categorías ya que se dificulta la lectura (variables policotómicas) y utilizar las variables ordinales.

Gráfico de barras (policotomicas): cada barra representa una categoría y su altura la frecuencia (absoluta o relativa), las barras deben estar separadas y es importante que el eje Y empiece en la frecuencia 0.

Pictogramas (policotómicas): es una forma de diagrama que en vez de utilizar barras se utiliza un dibujo o diseño relacionado con esa variable. Los errores usar frecuencia absoluta. Si se trata de variable   cuantitativa es preferible un histograma (polígono de frecuencia, tronoco y hojas…).

Variables cuantitativas

Gráfico de barras (sólo para variables discreta con bajo rango de valores).

Histogramas y poligonos de frecuencia (variables continuas). Sucesión de rectángulos continuos construidos sobre una recta, representa a una variable con sus datos agrupados en intervalos. El ancho o la base de cada rectángulo nos dice la amplitud de cada intervalo y la altura la frecuencia.  Cada intervalo representado en el histograma ocupa un rectángulo. Errores: confundirlo con un diagrama de Barras. Inapropiado para una variable continua y no tenerse en cuenta las diferentes amplitudes de los intervalos. 

Gráfico de tronco y hojas: híbrido entre la tabla de frecuencia e histograma, de manera que nos muestra la forma de la distribución y los valores de la variable. Cada dato de la serie se divide en dos partes: el tronco (decenas) y la hoja (unidades)

Datos bidimensionales y multidimensionales

Gráfico tendencias temporales (para datos bidimensionales): se denomina tendencia de una serie temporal a su comportamiento o movimiento a largo plazo, por ejemplo, el Número de transplantes realizados en Andalucía. Periodo 2010-2017.

Diagramas de dispersión (para datos bidimensionales). Scatter plot (Diagrama de dispersión, nube de puntos…). Para representar el comportamiento de dos variables continuas en un grupo de individuos. En el eje “x” se representa la variable independiente y en el eje “y” los valores de la variable dependiente. La imagen del diagrama nos da una posible idea de la correlación entre las dos variables.

Diagramas de estrellas (para datos muldimensionales): Para representar un conjunto de variables cuantitativas y comparar entre diferentes unidades de análisis (individuos o conglomerados). Cada variable representa un vértice del diagrama de estrella. Gráficamente da una idea del comportamiento conjunto de las variables estudiadas. También permite comparativas con un “gold standard”.

"La estadística es una ciencia que demuestra que, si mi vecino tiene dos coches y yo ninguno, los dos tenemos un coche".  

(George Bernard Shaw)

Hasta la próxima!!

 Almu❤

    

Tema 5: ESTADÍSTICOS UNIVARIABLES: MEDIDAS RESUMEN PARA VARIABLES CUANTITATIVAS: Medidas de tendencia central. Medidas de dispersión.Medidas de posición. Forma de distribución: asimétrica y curtosis.

Podemos resumir una serie de observaciones mediante "estadísticos": "función de los datos observados". Existen tres tipos de medidas estadísticas:

Medidas de tendencia central: dan idea de los valores al rededor de los cuales el resto de los datos tienen tendencia a agruparse. 

•  Media aritmética
•  La mediana (valor de la observación tal que un 50% de los datos es menor y un 50% es       mayor, si el numéro de observaciones es impar será (n/2)+1)           
• La moda (valor con mayor frecuencia, puede ser bidmodal, multimodal... y si los datos están    agrupados se habla de clase modal).

Medidas de posición: dividen un conjunto ordenado de datos en grupos con la misma cantidad de individuos. Los cuantiles solo tienen en cuenta la posición de los valores en la muestra. Los más  usados son:

• Percentiles: dividen la  muestra ordenada en 100 partes. Es "i" (Pi) aquel valor que ordenadas    las observaciones en forma creciente, el i% de ellas son menores que él y el (100-i)% son          mayores. En una serie de datos agrupados buscamos el intervalo en el que la frecuecia relativa  acumulada sea superior a valor del percentil. El valor del P50 corresponde al valor de la           mediana.
•  Deciles: divide la muestra ordenada en 10 partes. El i/ 10% de las observacions son menos que él y el (100-i)/10% son mayores. El valor D5 corresponde al valor de la mediana y al P50.
• Cuartiles: Divide la muestra ordenada en 4 partes. El Q1 muestra que el 25% de las                 observaciones son menores y el 75% mayores. el Q2 sería 50% mayores y 50% menores,         coincide con el valor de D5 y valor de la mediana P50. El Q3 sería el 75% son menores y el     25% mayores y el Q4 indica el valor mayor que se alcanza en la serie numérica.

Medidas de dispersión o variabilidad: dan información acerca de la heterogeneidad de nuestras observaciones. 

•  Rango o recorrido: diferencia entre el mayor y menor valor de la muestra [xn-x1]
•  Desviación media: media aritmética de las distancias de cada observación con respecto a la     media de la muestra
•  Desviación típica: cuantifica el error que cometemos si representamos una muestra                   únicamente por su media
• Varianza: misma información en valores cuadráticos
•  Recorrido intercuartílico: diferencia entre el tercer y primer cuartil
• Coenficiente de variación: compara la heterogeneidad de dos series numéricas de las unidades  de medidas.

Distribuciones normales: En estadística se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en fenómenos reales. La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de los valores posición central (media, mediana y moda, que coinciden en estas distribuciones). Esta curva se conoce como campana de Gauss.

Asimetrías y cuartosis: Coeficiente de asimetría de una variable: Grado de asimetría de la distribución de sus datos en torno a su media, es adimensional y adopta valores entre -1 y 1. G1= 0 (distribución simétrica), g1> 0 (distribución asimétrica positiva) y g1<0 (distribución asimétrica negatia).Coeficiente de apuntamiento o curtosis de una variable, sirve para medir el grado de concentración de los valores que toma 

en torno a su media, se elige como referencia una variable con distribución normal, de modo que para ella el coeficiente de curtosis es 0 y adopta también valores entre -1 y 1. G2=0 (distribución mesocúrtica), g2>0 (leptocúrtica) y g2 <0 (platiúrtica). 

TEMA 4: INTRODUCCIÓN A LA ESTADÍSTICA DESCRIPTIVA: Medidas resumen variables cualitativas. Medidas de frecuencia. Proporciones, razones y tasas. Construcción de tablas de frecuencia.

Existen dos conceptos de estadística: la estadística descriptiva que se encarga de ordenar, agrupar, clasificar datos de un determinado grupo, explorar las relaciones entre variables étc. de manera clara y fácil sin pretender sacar conclusiones de tipo general. La estadística inferencial, en cambio, predice el comportamiento de una población apoyándose de la estadística descriptiva y la probabilidad. Nosotros  trabajaremos  la estadística descriptiva. 

Variables: Presentación de datos.

Las tablas de frecuencia nos ayudan a leer los datos que muestran frecuencias en columnas y las categorías de las variables en filas. Presentan información repetitiva de forma visible y comprensible y además encontramos múltiples de variaciones (tabla de frecuencia variable cualitativa dicotómica,  policotómica, ordinal,  discreta...). 

Variables Continuas: tablas de frecuencia de datos agrupados.

La manera de hacer sería siguiendo estos pasos: 

1. Calculamos el Recorrido: 
   Re= X_n – X₁ = 6.1-3.3=2.8
2. Nº de intervalos, que se obtiene calculando la raiz cuadrada del nº de datos observados. 
3. La Amplitud se obtiene dividiendo el recorrido por el nº de intervalos. A= 2,8/6=0,42.

Una vez que tenemos esos datos, construimos la tabla y para ello deberíamos calcular la frecuencia absoluta (fi) que corresponde con el nº de individuos que están incluidos en un intervalo. Las frecuencias relativas (hi) que es la proporción de individuos referidos al total que presentan una modalidad o que están incluidos en un intervalo y se calcula dividiendo la frecuencia absoluta entre el nº total de datos y las frecuencias acumuladas (fi o hi) que es el nº de individuos menores o iguales que la modalidad o el intervalo que estamos estudiando. Por último también podemos completar nuestra tabla con la marca de clase que corresponde al punto medio de los intervalos de clase. Aquí tendríamos la tabla completa:

• Indicadores/ Concepto de indicador: medida de la frecuencia de un determinado suceso en una población, expresado como un número que puede ser una proporción, una tasa, una razón u Odds. Están formados por un numerador y un denominador, es decir, es el resultado del cociente entre dos magnitudes.
• Proporciones: Comparación a través de un cociente (división) entre un subconjunto y el conjunto al que pertenece. Por ejemplo, la proporción de personas que presentan una enfermedad. (Nº de enfermos/ Nº total de individuos)
• Tasas (Rate): Comparación a través de una división, entre el número de veces que ocurre en un cierto tipo de evento y la población en la que puede ocurrir dicho evento en un tiempo determiando. Usualmente el resultado es una cifra fraccionaria menor de 1 y suele ser multiplicado.
• Incidencia: Nº de nuevos casos de enfermedad que ocurren en un periodo de tiempo específico en una población a riesgo de desarrollar una enfermedad. Mide cambios y es por tanto, una medida de riesgo.

La incidencia acumulada (proporción de incidencia) es el riesgo de que se produzca el suceso. Se calcula utilizando un periodo de tiempo el cual consideramos que todos los individuos  de la población están a riesgo de la enfermedad. No puede haber pérdidas de seguimiento ya que se siguen a todos los sujetos mediante el periodo y no permite inferir fuera del periodo de estudio. Mide la probabilidad de tener el evento:

Con frecuencia, no todos los individuos a riesgo (denominador) son seguidos durante el mismo periodo de tiempo. Si se dispone de los diferentes tiempos de observación ("tiempos en riesgo") de los diferentes individuos, se puede calcular la densidad de incidencia o tasa de incidencia. Especificaríamos la unidad de tiempo y la "tasa" a la cual ocurren los eventos en sujetos de la población en riesgo en cualquier momento. 

• Razones o "Ratios": consiste en la comparación a través de una división entre dos conjuntos distintos, es decir, el numerador del cociente no está incluido en el denominador.
• ODDS o ventaja: consiste en el cociente entre la proporción o probabilidad de ocurrencia de un evento y la proporción o probabilidad de no ocurrencia. La Odds representa la frecuencia de un aspecto relativo a los sujetos que no presentan dicho aspecto, por lo que es un tipo especial de razón. Sus valores van de 0 hasta el infinito.

Medidas de asociación: relaciones entre proporción, ratios y Odds.

Se llama medidas de asociación a la magnitud de asociación entre dos fenómenos. Las tres más importantes son:

 1. Razón de prevalencia: estudios descriptivos de corte transversal. Realiza un ratio entre dos prevalencias (proporciones)

  2. Riesgo relativo o razón de riesgos: estudios de observación de seguimientos o estudios experimentales. Realiza un ratio entre dos incidencias acumuladas (proporciones) o dos densidades de incidencia (tasas)

3. Odds ratio: estudios de casos y controles. Realiza una ratio entre dos medidas "odds" o ventajas.